Procedure / Set Up:
The experiment is broken up into two parts
Part 1: We will be performing 6 different experiments/ trials and measuring the angular acceleration of each one as well looking at how various changes in the experiment effect the angular acceleration of our system. In addition we will use one of our trials and look at v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk)
Before beginning the actual experiment, a few measurements needed to be made using a pair of calipers and an electronic balance.
To begin, clean all the disks with alcohol before using the apparatus. Plug in the power supply to the apparatus and connect it to Logger Pro. Be sure to choose the rotary sensor and set the sensor settings to 200 counts per rotation, as there are 200 marks on the top disk. The hose clamp on the bottom of the apparatus should be open in order for the disks to rotate independently of each other. Turn on the compressed air, but just enough to keep thing smooth and with the string wrapped around the torque pulley and the hanging mass is at its highest point, hit collect on Logger Pro. Taking the slope of the graph of angular velocity vs. time can be done to determine the angular acceleration of the system. This will be done for all 6 trials.
Important Note:
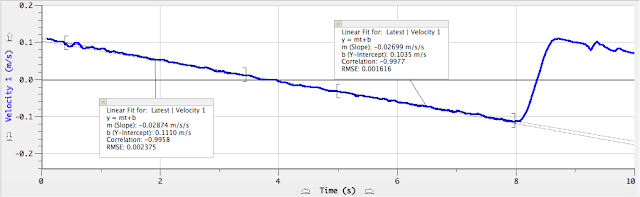
We take an average angular acceleration from the up and down motion because when the mass descends, there is frictional torque slowing down the disk and torque from the string speeding up the disk. When the mass ascends, there is frictional torque from the disks and frictional torque from the string slowing down the disk.
Below is an image better explaining this complication.
After completing each trial, there should be 6 different recorded angular acceleration values. Below are two examples of our data analysis for part 1. Each trial looks pretty much the same.
Effects to look at by various changes in the experiment for each trial.
Trial 1, 2, and 3: Effects of changing the hanging mass
Trial 1 and 4: Effects of changing the radius at which the hanging mass exerts a torque
Trial 4, 5, and 6: Effects of changing the rotating mass (disks).
Trial 2:
2 x hanging mass
Small torque pulley
Top Steel disk
Taking the slope of the angular velocity vs. time will yield the angular acceleration. α = 1.259 rad/s^2 for this trail.
Trial 5:
hanging mass only
Large torque pulley
Top aluminum disk
Again, taking the slope of the angular velocity vs. time graph gives the angular acceleration. α = 3.444 rad/s^2
Compiled data shown below:
For experiment 6 we added a motion sensor to our set up to compare v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk)
This graph represents v (hanging mass) vs time and by taking the slope of the up and down motion, we were able to get a (hanging mass).
Below is the graph of v (hanging mass) vs time. By taking the mean of the up and down values, we can get v average.
Below is a graph of ω (disk) vs. time and again taking the mean of the up and down values, we can get ω average.
Using the same method in determining the average acceleration of our system, we can get v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk).
Conclusion Part 1: By various changes in the configuration of the apparatus, we noticed that the greater the hanging mass the greater the angular acceleration. Experiment 2 had 50 grams of hanging mass with an angular acceleration of 1.259 rad/s^2 and experiment 1 had 25 grams of hanging mass with an angular acceleration of 0.6274 rad/s^2. Another observation was that as the radius of the torque pulley is increased, the larger the value of angular acceleration would be. Experiment 1 had a smaller torque pulley radius and an angular acceleration of 0.6274 rad/s^2, while experiment 4 had the larger radius with angular acceleration of 1.217 rad/s^2. One last observation made was that the more massive the rotating disks, the slower the angular acceleration was. Experiment 5 used an aluminum disk and generated an angular acceleration of 3.444 rad/s^2 while experiment 6 used a steel disk and generated an angular acceleration of 0.641 rad/s^2.
Part 2: Use our data from part 1 to calculate an experimental moment of inertia and compare it to a theoretical moment of inertia.
Because our system is not completely frictionless, α isn't the same when the mass ascends and descends. Below is a simple derivation of how we will calculate an experimental moment of inertia. The theoretical moment of inertia is simply the moment of inertia of a disk.
Below is our experimental moments of inertia vs. theoretical moments of inertia.
Conclusion part 2: As you can see, our experimental and theoretical values do not match at all. There is a 78% error from experiment 1 and similarly for experiment 2. This is an extremely high error.
Overall Conclusion:
In part 1, we measured the angular acceleration of a system by applying a known torque. We looked at the effects on α by varying the configuration and compared them to each other. We set up a motion sensor to look at v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk). In part 2, we used our values from part 1 to calculate an experimental moment of inertia and compare it to a theoretical value of moment of inertia. As observed, our values did not compare well, all the data from part 1 seemed correct.
Error in our values could have been due to not setting the rotary sensor to read 200 marks. At one point in our trials, we realized we had the wrong disk on top and had to restart, which could have possibly caused us to forget to change the sensor settings back to 200 marks. Another source of error could have been from improperly handling the disks. We made sure to clean them with alcohol, but as we were swapping them we put finger prints all over to bottom and top of the disks. Over all, the final results of our experiment did not come out as precise as we had hoped.
No comments:
Post a Comment