5/20/15: Conservation of Energy / Conservation of Angular Momentum Lab 19

Purpose: Predict how high a pivoted clay-stick combination will rise, after inelastically colliding with a stationary blob of clay.

Procedure / Set Up:

The apparatus consists of a meter stick with a hole drilled at one end (pivot), and is fastened onto a small device that will allow the stick to rotate freely. Tape is wrapped, sticky side out, at the end of the stick so that when it collies with a stationary blob of clay, also wrapped sticky side out, it will create an inelastic collision.                                                                                                                                         Our Job is to predict how high the clay-stick combination will rise after being released from a horizontal position by using conservation of energy and conservation of angular momentum.

We will then use Logger Pros video capture software along with a camera to find the max height and compare it to our predicted value.  

Prediction (Experimental Value):

Before predicting the max height, we will need the mass of the stick, the mass of the clay, and the length of the stick from the pivot point.

M = .103 kg (Mass of Stick)

m = .025 kg (Mass of Clay)

length from the pivot is 0.99 meters. 

We know that the moment of inertia pivoted at one end is 1/3 ML^2, but the pivot is not exactly at the end of the stick. Instead we will need to use the parallel axis theorem when performing our calculations. 

We can predict the max height by splitting the problem into 3 separate parts.

1. The angular velocity just before impact. (Conservation of Energy)

2. The angular velocity right after impact. (Conservation of Angular Momentum)

3. The angle the stick + clay makes with the vertical. (Conservation of Energy)

Part 1: Conservation of Energy

By raising the stick to a horizontal position, we give it potential energy and when released, the potential energy is converted into rotational energy. Below we use conservation of energy and the parallel axis theorem for just the stick to find ω. We set the horizontal position of the stick, just before being released, to be at 0 GPE. ω = 5.45 rad/s

Part 2: Conservation of Angular Momentum

Since the stick is rotating about a pivot and colliding with a blob of clay it is useful to use conservation of angular momentum and the parallel axis theorem as well as our value of ω from part 1 to find ω right after to collision. it make sense for ω to be less, since the stick is inelastically colliding with a stationary blob of clay. ω = 3.14 rad/sec

Part 3: Conservation of Energy

Because we are including the angle the (stick + clay) makes with the vertical we will need to write ø in terms of h, which is what we are trying to solve for. Below h' is the height we are looking for. We determined h' = 0.365m

Video Capture (Theoretical Value):

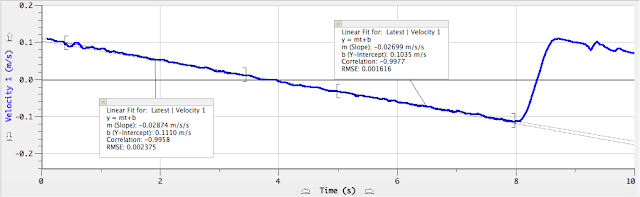
Now that we have found an experimental value for the max height, we will use Logger pro to find the theoretical value. The apparatus is exactly the same, but we are adding a camera to capture the stick as is swings and collides with the clay and rises to some height.

After capturing the motion of the stick, we analyzed the video and determined the theoretical max height to be 0.3795 m.

Comparing the theoretical and experimental values:

Experimental value: 0.3765 m

Theoretical value: 0.3795 m

By comparing our values, we were well within the range we had determined using Logger Pro. After performing a percent error calculation, we found only a 0.7905 % error.

Conclusion:

Our goal was to determine the max height a pivoted clay-stick combination will rise after inelastically colliding with a stationary blob of clay. We were able to approach the problem using conservation of energy and conservation of angular momentum. Since we did not know the moment of inertia about the pivoted point, we needed to include the parallel axis theorem in our calculations. Although our percent error was quite low, it could have included friction from the pivot or small errors when analyzing the video. Over all the experiment was a success. We were able to experimentally predict the max height and it compared well to the theoretical value. 

5/4/15: Angular Acceleration Lab 16

Purpose: Apply a known torque to an object that can rotate and measure the angular acceleration. Use the measured angular acceleration to calculate an experimental moment of inertia and compare it to a theoretical value of moment of inertia.

Procedure / Set Up:

The set up consists of 2 stacked disks that are placed adjacent to a Pasco rotational sensor. On top of the disks is a torque pulley with a string wrapped around it. The string is attached to a hanging mass which goes over another pulley at the edge of the apparatus. When the compressed air is turned on, the disks rotate independently and the hanging mass moves up and down.

The experiment is broken up into two parts

Part 1: We will be performing 6 different experiments/ trials and measuring the angular acceleration of each one as well looking at how various changes in the experiment effect the angular acceleration of our system. In addition we will use one of our trials and look at v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk)






Before beginning the actual experiment, a few measurements needed to be made using a pair of calipers and an electronic balance. 

To begin, clean all the disks with alcohol before using the apparatus. Plug in the power supply to the apparatus and connect it to Logger Pro. Be sure to choose the rotary sensor and set the sensor settings to 200 counts per rotation, as there are 200 marks on the top disk. The hose clamp on the bottom of the apparatus should be open in order for the disks to rotate independently of each other. Turn on the compressed air, but just enough to keep thing smooth and with the string wrapped around the torque pulley and the hanging mass is at its highest point, hit collect on Logger Pro. Taking the slope of the graph of angular velocity vs. time can be done to determine the angular acceleration of the system. This will be done for all 6 trials.

Important Note:

We take an average angular acceleration from the up and down motion because when the mass descends, there is frictional torque slowing down the disk and torque from the string speeding up the disk. When the mass ascends, there is frictional torque from the disks and frictional torque from the string slowing down the disk.

Below is an image better explaining this complication.  

 

After completing each trial, there should be 6 different recorded angular acceleration values. Below are two examples of our data analysis for part 1. Each trial looks pretty much the same. 

Effects to look at by various changes in the experiment for each trial.

Trial 1, 2, and 3: Effects of changing the hanging mass

Trial 1 and 4: Effects of changing the radius at which the hanging mass exerts a torque

Trial 4, 5, and 6: Effects of changing the rotating mass (disks).

Trial 2: 

2 x hanging mass

Small torque pulley

Top Steel disk

Taking the slope of the angular velocity vs. time will yield the angular acceleration. α = 1.259 rad/s^2 for this trail.

Trial 5:

hanging mass only

Large torque pulley

Top aluminum disk

Again, taking the slope of the angular velocity vs. time graph gives the angular acceleration. α = 3.444 rad/s^2

Compiled data shown below:

For experiment 6 we added a motion sensor to our set up to compare v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk)

This graph represents v (hanging mass) vs time and by taking the slope of the up and down motion, we were able to get a (hanging mass).

 This graph represents ω (disk) vs. time and again taking the slope will give us α (disk).

Below is the graph of v (hanging mass) vs time. By taking the mean of the up and down values, we can get v average.

Below is a graph of ω (disk) vs. time and again taking the mean of the up and down values, we can get ω average.

Using the same method in determining the average acceleration of our system, we can get v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk).

Conclusion Part 1: By various changes in the configuration of the apparatus, we noticed that the greater the hanging mass the greater the angular acceleration. Experiment 2 had 50 grams of hanging mass with an angular acceleration of 1.259 rad/s^2 and experiment 1 had 25 grams of hanging mass with an angular acceleration of 0.6274 rad/s^2. Another observation was that as the radius of the torque pulley is increased, the larger the value of angular acceleration would be. Experiment 1 had a smaller torque pulley radius and an angular acceleration of 0.6274 rad/s^2, while experiment 4 had the larger radius with angular acceleration of 1.217 rad/s^2. One last observation made was that the more massive the rotating disks, the slower the angular acceleration was. Experiment 5 used an aluminum disk and generated an angular acceleration of 3.444 rad/s^2 while experiment 6 used a steel disk and generated an angular acceleration of 0.641 rad/s^2.

Part 2: Use our data from part 1 to calculate an experimental moment of inertia and compare it to a theoretical moment of inertia.

Because our system is not completely frictionless, α isn't the same when the mass ascends and descends. Below is a simple derivation of how we will calculate an experimental moment of inertia. The theoretical moment of inertia is simply the moment of inertia of a disk. 

Below is our experimental moments of inertia vs. theoretical moments of inertia. 

Conclusion part 2: As you can see, our experimental and theoretical values do not match at all. There is a 78% error from experiment 1 and  similarly for experiment 2. This is an extremely high error. 

Overall Conclusion:

In part 1, we measured the angular acceleration of a system by applying a known torque. We looked at the effects on α by varying the configuration and compared them to each other. We set up a motion sensor to look at v (hanging mass) vs. ω (disk) and a (hanging mass) vs. α (disk). In part 2, we used our values from part 1 to calculate an experimental moment of inertia and compare it to a theoretical value of moment of inertia. As observed, our values did not compare well, all the data from part 1 seemed correct.

Error in our values could have been due to not setting the rotary sensor to read 200 marks. At one point in our trials, we realized we had the wrong disk on top and had to restart, which could have possibly caused us to forget to change the sensor settings back to 200 marks. Another source of error could have been from improperly handling the disks. We made sure to clean them with alcohol, but as we were swapping them we put finger prints all over to bottom and top of the disks. Over all, the final results of our experiment did not come out as precise as we had hoped. 

5/13/15: Moment of Inertia of a Uniform Triangle Lab 17

Purpose: Determine the moment of inertia of a right triangular thin plate around its center of mass, for two perpendicular orientations of the triangle. We will compare an experimental value of moment of inertia to a theoretical value of moment of inertia. 

Procedure / Set Up:

The set up consists of 2 stacked disks that are placed adjacent to a Pasco rotational sensor. On top of the disks is a torque pulley with a string wrapped around it as well as triangle mounted on a holder. The string is attached to a hanging mass which goes over another pulley at the edge of the apparatus. When the compressed air is turned on, the disks rotate independently and the hanging mass moves up and down.

Approach - Theory:

We want to calculate the moment of inertia about the center of mass of a thin triangular plate, but because the limits of integration are simpler if we calculate the moment of inertia around a vertical end of the triangle, we can calculate that moment of inertia and use the parallel axis theorem to then get the moment of inertia around the center of mass.

The parallel axis-theorem is give by:

Since we will be calculating the moment of inertia of the triangular plate in two different orientations, upright and sideways, the tension in the string will exert a torque on the pulley-disk combination and by measuring the angular acceleration of the system we can determine the moment of inertia of the system. We will accomplish this by measuring α of the (disk + holder), α of (disk + holder + triangle), determining I of (disk + holder), I of (disk + holder + triangle), and the difference between the two moments of inertia will give us the moment of inertia of the triangle. These will be our experimental values for I. In total, we will compare four different values.  

Before beginning the experiment, we derived and expression for (I around cm), which will be our theoretical value. By using the parallel axis theorem, I = 1/18 ML^2
This equation for I will be the same for both the upright and sideways orientations. 
where M = 0.455 g, L = 0.0983 m (upright), L = 0.1493 m (sideways)

Because of frictional torque in the system, the rotating disk isn't truly frictionless and there is mass is the frictionless pulley. We derived an expression for the the moment of inertia of the system following this approach back in the angular acceleration lab. The derivation is shown below. The boxed equation on the bottom left is the one to notice.

Now we can measure α of the (disk + holder), α of (disk + holder + triangle), and determine I of (disk + holder) and I of (disk + holder + triangle).

Upright Triangle:

How the setup should look at this point for α of the (disk + holder).

α of the (disk + holder) was determined by allowing the mass to rise up and down while Logger Pro generated the angular velocity graph.The slope of ω vs. t would give us the α. 

An average was taken of α up and α down in order to find α of the system. I of (disk + holder) was then calculated as shown below. I = 9.237 x 10^-4 kg*m^2

Using the same logic as above, I of (disk + holder + triangle) was calculated as shown below.

Graph of ω vs. t for (disk + holder + triangle) to find α

Using α to find I (disk + holder + triangle) calculation.

The difference between the two moments of inertia will give us the experimental moment of inertia of the upright triangle. I = 2.482 x 10^-4 kg*m^2. Using the theoretical derivation I = 1/18 ML^2, we concluded I = 2.44 x 10^-4 kg*m^2. Comparing these two values, we get a percent error of 1.721 %.

Sideways triangle: 

How to set up should look:

Once again α of the (disk + holder) was determined by allowing the mass to rise up and down while Logger Pro generated the angular velocity graph.The slope of ω vs. t would give us the α. I (disk + holder) is the same value as was in the upright triangle I = 9.237 x 10^-4 kg*m^2.

The same logic was applied as from the upright triangle. α of the system (disk + holder + triangle) was determined by taking an average of α up and α down from the slope of the ω vs. t graph.

The difference of I of (disk + holder) and I of (disk + holder + triangle) would give us the experimental value of I for the sideways triangle. Below are the calculations.

By comparing the experimental value I = 5.587 x 10^-4 kg*m^2 and the theoretical value I = 5.634 x 10^-4 kg*m^2, we se we have a percent error of  0.834 %.

Conclusion: 

Our goal was to determine the moment of inertia of a triangular plate in two different orientations. We were able to achieve this by using the parallel axis theorem. We derived an expression for the moment of inertia, measured α of the system, calculated I of the system, and lastly compared an experimental value to a theoretical value. Our percent error for both orientations was relatively low, so it is safe to say the experiment was a success. An error we encountered at first was that our percent error for the sideways triangle was relatively high, but it was easily fixed by remeasuring the length of one of the sides of our triangle. 

5/11/15: Moment of Inertia and Frictional Torque Lab 18

Purpose: Use Newtons second law of rotation to determine the time it takes for a cart to travel down an incline while attached to a large metal disk by a string.

Procedure / Set up:

The apparatus consists of a large disk on a central shaft and at the center of the disk are smaller cylindrical disks that serve as an axis of rotation.

As the cart is traveling down the incline, the disk exerts a frictional torque opposite the carts direction of motion. So before actually predicting the time it would take for the cart to travel 1m, we need to measure the frictional torque exerted by the apparatus. To accomplish this, we will need to determine the total moment of inertia and the angular acceleration of the apparatus. (T frictional = Iα)

Determining the total moment of inertia:

Measure and record the dimensions of the larger central disk and the two smaller side cylindrical disks. These values will be used to determine the volume of each piece. The smaller disks are labeled (1) and (3) and the larger disk is labeled (2). 

The ratio of the volume for a piece divided by the total volume of the apparatus will give us the percentage of mass for that piece. For example if 86 % of the total mass of the apparatus belongs to the central disk, then we can take that value and multiply it by the total mass of the apparatus to find the mass of just that central disk. The total moment of inertia is the sum of the moment of inertia of the central disk plus the two moments of inertia for the smaller cylindrical disks. 

Determining the angular acceleration:

We set up a camera so that its lens lines up directly with the apparatus' axis of rotation.

Our plan was to capture the disk as it rotates and use the Logger Pro video capture software to find the angular deceleration of the disk. To do this, we marked a point on the disk, recored the disk while it spun, and analyzed the video. During the analyzation process we plotted a point every time our marked spot on the disk went through one revolution or 2π radians. We did this for 15 revolutions or 30π radians. By plotting a point every revolution, Logger Pro would automatically create a column for the time is took to complete that revolution. We next created a column titled theta (ø). This column consisted of the number of radians traveled by the point every 2π revolutions/increments. We next plotted a graph of ø vs. t to find the angular acceleration of the disk.

The equation ø = At^2 + Bt + C is very similar ø = 1/2αt^2 + ωt, Therefore 2A is our actual value for angular acceleration, which equates to -1.075 rad/s.

Because T = Iα, we can now say our value for frictional torque is -0.02265 N*m.

Determining the time it takes the cart to travel down the incline:

The set up consists of the apparatus along with a track at the edge of the table, with the track inclined around 44º. A string is tied around the smaller cylindrical disk and then tied to a cart. The track is positioned so that it is parallel to the string.

Before running the experiment we are asked to predict the time it will take the cart to travel 1m. By drawing a free body diagram of the situation and using Newtons second law of rotation and along with kinematics, the time we determined it would take the cart to travel 1m was 9.42 seconds. 

With our predicted value at hand we performed four trials and recored the times for each.

T1: 9.38 s

T2: 9.50 s

T3: 9.44 s

T4: 9.41 s

These values averaged to 9.432 seconds, which gave us a percent error of 0.127 %

Conclusion:

In this lab, our main goal was to determine the time it would take a cart to travel down an incline when attached to cylindrical rotating disk. We were able to find this value using concepts from Newtons second law of rotation, moment of inertia, kinematics, and rotational kinematics. The main steps were calculating the total moment of inertia of the apparatus, measuring the angular deceleration of the apparatus with Logger Pro video capture, and deriving an equation that would express the linear acceleration of the cart enabling us to find the time. The more difficult part of the lab was coming up with a method for finding the angular deceleration of the apparatus. Although our final error was relatively small, error could have been introduced from uncertainty in measurements or from unaccounted friction from the track.